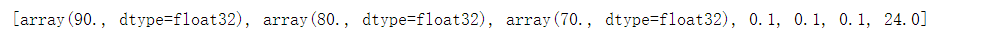初识 TensorFlow

1. 了解引入的需要神经网络解决的问题
2. 学习用神经网络的基本结构、表达方式和编程实现
3. 学习训练神经网络的基本方法

三好学生成绩问题

总分 = 德育分 * 60% + 智育分 * 30% + 体育分 * 10%

假设家长不知道这个规则，已知：

• 学校一定是以德育分、智育分和体育分三项分数的总分来确定三好学生的
• 计算总分时，三项分数应该有各自的权重系数
• 各自孩子的三项分数都已经知道，总分也已经知道

经过家长们的分析，只有三项分数各自乘以的权重系数是未知的。问题演变成求解方程：w1x + w2y + w3z = A 中的三个 w 即权重。其中 x、y、z、A 分别对应几位学生的德育分、智育分、体育分和总分。

两个方程式解三个未知数无法求解：

90w1 + 80w2 + 70w3 = 85
98w1 + 95w2 + 87w3 = 96

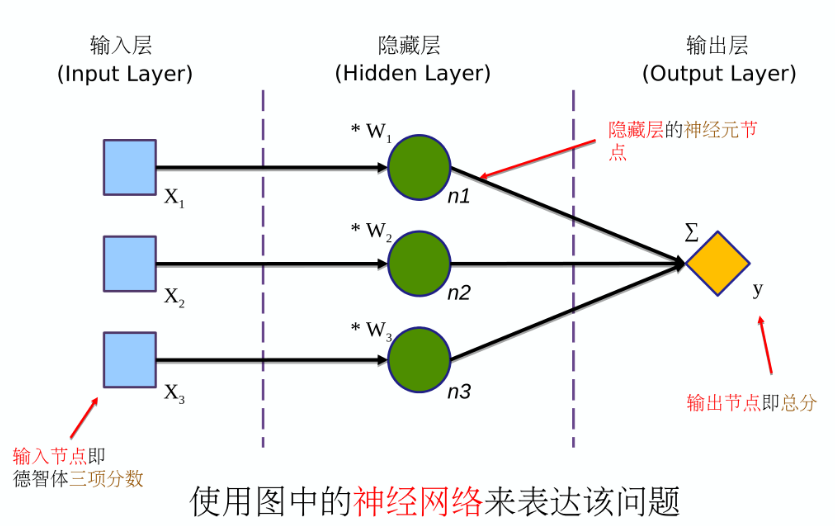
搭建对应的网络神经

神经网络模型图的一般约定：

• 神经网络图一般包含一个输入层、一个或多个隐藏层，以及一个输出层
• 输入层是描逑输入数据的形态的（输入节点）
• 隐藏层是描迒神经网络模型结构中最重要的部分隐藏层可以有多个；每一层有一个或多个神经元（神经元节点/节点）；每个节点接收上层的数据并进行运算向下层输出数据（计算操作/操作）
• 输出层一般是神经网络的最后一层，包含一个或多个输出节点

神经网络的代码：

import tensorflow as tf

x1 = tf.placeholder(dtype = tf.float32)
x2 = tf.placeholder(dtype = tf.float32)
x3 = tf.placeholder(dtype = tf.float32)

w1 = tf.Variable(0.1, dtype = tf.float32)
w2 = tf.Variable(0.1, dtype = tf.float32)
w3 = tf.Variable(0.1, dtype = tf.float32)

n1 = x1 * w1
n2 = x2 * w2
n3 = x3 * w3

y = n1 + n2 + n3

sess = tf.Session()
init = tf.global_variable_initializer()

sess.run(init)

result = sess.run([x1, x2, x3, w1, w2, w3, y], feed_dict={x1: 90, x2: 80, x3: 70})
print(result)

其中

x1 = tf.placeholder(dtype = tf.float32)
x2 = tf.placeholder(dtype = tf.float32)
x3 = tf.placeholder(dtype = tf.float32)

通过 tf.placeholder 定义三个占位符（placeholder），作为神经网络的输入节点，来准备分别接收德育、智育、体育三门分数作为神经网络的输入。dtype 是 data type 的缩写，dtype = tf.float3 是命令参数，tf.float32 代表 32 位小数。

w1 = tf.Variable(0.1, dtype = tf.float32)
w2 = tf.Variable(0.1, dtype = tf.float32)
w3 = tf.Variable(0.1, dtype = tf.float32)

通过 tf.Variable() 定义三个可变参数。

n1 = x1 * w1
n2 = x2 * w2
n3 = x3 * w3

n1、n2、n3 是三个隐藏层节点，实际上是他们的计算算式。

y = n1 + n2 + n3

定义输出节点 y，也就是总分的计算公式（加权求和）。至此，神经网络模型的定义完成。

sess = tf.Session()

定义神经网络的会话对象

init = tf.global_variable_initializer()

tf.global_variable_initializer() 返回专门用于初始化可变参数的对象。

sess.run(init)

初始化所有的可变参数。

result = sess.run([x1, x2, x3, w1, w2, w3, y], feed_dict={x1: 90, x2: 80, x3: 70})
print(result)

[x1, x2, x3, w1, w2, w3, y] 为要查看的结果项，feed_dict={x1: 90, x2: 80, x3: 70} 为输入的数据。输入三门分数运行神经网络并获得该神经网络输出的节点值。

运行代码，查看结果：

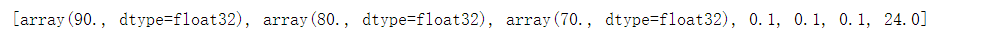
根据随意设置的可变参数初始值计算出的输出结果正确，证明搭建的神经网络可以运行，但不能真正投入使用，存在一定误差。

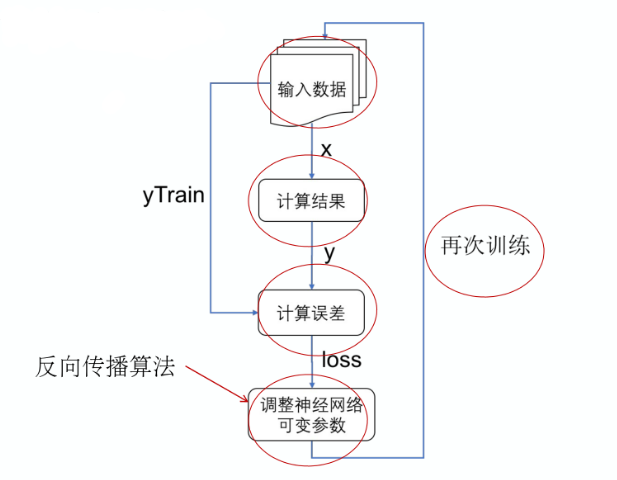
训练神经网络

神经网络在投入使用前，都要经过训练（train）的过程才能有准确的输出。

• 神经网络训练时一定要有训练数据
• 有监督学习中，训练数据中的每一条是由一组输入值和一个目标值组成的
• 目标值就是根据这一组输入数值应该得到的 “准答案”
• 一般来说，训练数据越多、离散性（覆盖面）越强越好

x1 = tf.placeholder(dtype = tf.float32)
x2 = tf.placeholder(dtype = tf.float32)
x3 = tf.placeholder(dtype = tf.float32)

yTrain = tf.placeholder(dtype = tf.float32)

给神经网络增加一个输入项 —— 目标值 yTrain，用来表示正确的总分结果。增加误差函数 loss，优化器 optimizer 和训练对象 train。

y = n1 + n2 + n3

loss = tf.abs(y - yTrain)
optimizer = tf.train.RMSPropOptimizer(0.001)
train = optimizer.minimize(loss)

tf.abs 函数用于取绝对值：计算结果 y 与目标值 yTrain 之间的误差。使用 RMSProp 优化器其中参数是学习率。optimizer.minimize 让优化器按照把 loss 最小化的原则来调整可变参数。

“误差函数”（又叫损失函数）用于让神经网络来判断当前网络的计算结果与目标值（也就是标准答案）相差多少。“训练对象”被神经网络用于控制训练的方式，常见的训练的方式是设法使误差函数的计算值越来越小。

result = sess.run([train, x1, x2, x3, w1, w2, w3, y, yTrain], feed_dict={x1: 90, x2: 80, x3: 70, yTrain: 96})
print(result)

训练两次并查看输出结果，注意与前面的区别：训练时要在 sess.run 函数的第一个参数中添加 train 这个训练对象；在 feed_dict 参数中多指定了 Train 的数值。

w1、w2、w3 和计算结果 y 已经开始有了变化。

循环进行多次训练：

for i in range(5000):
    result = sess.run([train, x1, x2, x3, w1, w2, w3, y, yTrain], feed_dict={x1: 90, x2: 80, x3: 70, yTrain: 85})
    print(result)

    result = sess.run([train, x1, x2, x3, w1, w2, w3, y, yTrain], feed_dict={x1: 98, x2: 95, x3: 87, yTrain: 96})
    print(result)

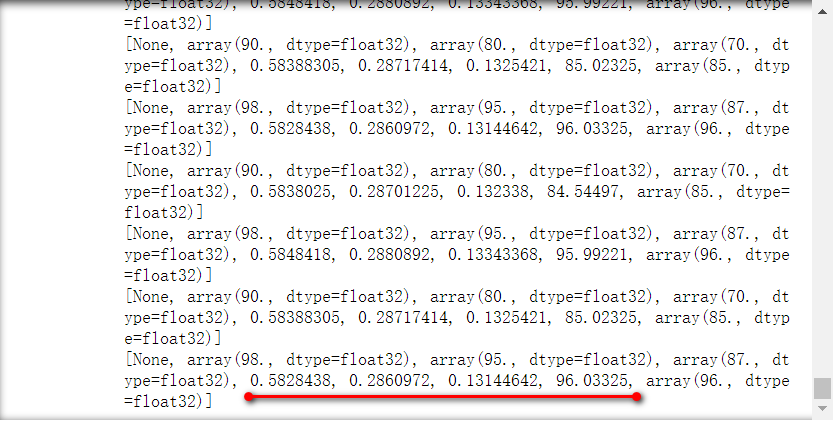
w1、w2、w3 已经非常接近于预期的 0.6、0.3、0.1，y 也非常接近目标值。

如果你使用了 TensorFlow 2.x，上述代码中可能存在兼容问题，但是可以通过更改部分代码解决：

# import tensorflow as tf
import tensorflow.compat.v1 as tf

tf.disable_v2_behavior()

x1 = tf.placeholder(dtype = tf.float32)
x2 = tf.placeholder(dtype = tf.float32)
x3 = tf.placeholder(dtype = tf.float32)

yTrain = tf.placeholder(dtype = tf.float32)

w1 = tf.Variable(0.1, dtype = tf.float32)
w2 = tf.Variable(0.1, dtype = tf.float32)
w3 = tf.Variable(0.1, dtype = tf.float32)

n1 = x1 * w1
n2 = x2 * w2
n3 = x3 * w3

y = n1 + n2 + n3

loss = tf.abs(y - yTrain)
optimizer = tf.train.RMSPropOptimizer(0.001)
train = optimizer.minimize(loss)

sess = tf.Session()
# init = tf.global_variables_initializer()
init = tf.compat.v1.global_variables_initializer()

sess.run(init)

for i in range(5000):
    result = sess.run([train, x1, x2, x3, w1, w2, w3, y, yTrain], feed_dict={x1: 90, x2: 80, x3: 70, yTrain: 85})
    print(result)

    result = sess.run([train, x1, x2, x3, w1, w2, w3, y, yTrain], feed_dict={x1: 98, x2: 95, x3: 87, yTrain: 96})
    print(result)